Der goldene Schnitt

Die Geometrie

Das Gegenteil der Symmetrie ist die Asymmetrie. Bei der Betrachtung einer Strecke gibt es neben einer einzig möglichen symmetrischen Aufteilung des Ganzen unendlich viele asymmetrische Teilungsmöglichkeiten. Unter diesen unzählbaren ungleichen Trennungen tritt nun eine auf, deren Einzigartigkeit und Besonderheit immer wieder die Aufmerksamkeit auf sich zog.

Abb. 4: Die asymmetrische Proportion des Goldenen SchnittesMinor : Major = Major : Ganzes

Man teilt eine Strecke so in zwei Teile, dass der kleinere Teil (Minor) sich zum größeren Teil (Major) genau so verhält wie der größere Teil wiederum zum Ganzen (Abb. 4). Anders ausgedrückt: Der proportionale Größenunterschied oder das Verhältnis zwischen Minor und Major ist gleich dem zwischen Major und dem Ganzen. Es handelt sich somit um eine Teilung, bei der immer ein Bezug auf das nächst Größere und somit schließlich auf das Ganze besteht. Gerade durch die Teilung wird der Bezug zum Ganzen herausgestellt. Das klingt erst einmal paradox, denn unter Teilung verstehen wir die Zerstörung des Ganzen. Die Proportion des goldenen Schnittes vollbringt das Paradoxon zwischen Teilung und Rückbezug auf das Ganze in beeindruckender Art und Weise.

Diese auch als Proportio divina oder göttliche Proportion bezeichnete Aufteilung übt schon seit Jahrtausenden eine besondere Anziehung auf die Menschen aus. Sie findet sich, wie später erläutert, in zahlreichen antiken Bauwerken, Gemälden und erstaunlicherweise auch in der Natur immer wieder. Geometrisch findet sich das Maß des goldenen Schnittes im Fünfstern, dem Pentagramm mehrfach wieder (Abb. 5). Ihm wurde zu allen Zeiten eine magische Wirkung zugeschrieben. Noch heute finden wir dieses Symbol in den Staatsfahnen in über 40 Ländern der Erde, u. a. in der USA.

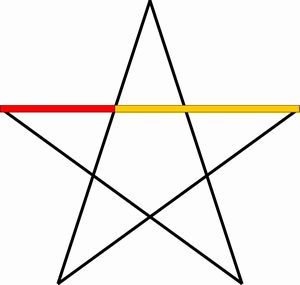Abb. 5: Das Pentagramm und der Goldene Schnitt

Die Schönheit des goldenen Schnittes

Es stellt sich die Frage, warum das Vorkommen des goldenen Schnittes immer wieder mit der Schönheit in Verbindung gebracht wurde und immer noch wird. Das Prinzip der Gleichheit und Einheit spielt dabei die Schlüsselrolle. Im goldenen Schnitt entsteht das Bild der Vollkommenheit nun jedoch nicht mehr durch die Gleichheit der Teile, sondern durch die Gleichheit der Proportionen. Die Verhältnisse der Teile Minor zur Major und Major zum Ganzen sind immer gleich. Die Einheit der Proportionen vermittelt das Bild der Vollkommenheit und lässt uns die Asymmetrie der Teile als harmonisch empfinden. Offensichtlich hängt das mit einer Symmetrie zusammen, die die Asymmetrie integriert: Die Symmetrie findet sich innerhalb das goldenen Schnittes nicht mehr in einer förmlichen Umsetzung (Gleichheit der Teile), sondern in einer verhältnismäßigen. Die Proportionen der einzelnen Elemente sind gleich. Im goldenen Schnitt ist das Verhältnis symmetrisch. Es ist die Symmetrie der Teile zu Gunsten der Symmetrie der Proportionen untergegangen.

Beeindruckenderweise taucht jedoch auch im goldenen Schnitt bei aufmerksamer Betrachtung die Symmetrie der Teile doch wieder auf. Dies wird optisch leichter nachvollziehbar, wenn man die drei Größen Minor, Major und das Ganze nebeneinander stellt (Abb. 6). Auf diese Weise findet sich auch in der Geometrie des goldenen Schnittes eine Symmetrieachse wieder. Ein weiteres Paradoxon tut sich auf: Im scheinbar absolut asymmetrischen Verhältnis der Proportio divina verbirgt sich gleich zweimal die Symmetrie, zum einen in der Gleichheit der Proportionen (Minor : Major) und zum anderen in der Gleichheit der Teile (Symmetrie), wie sie in Abbildung 6 zum Ausdruck kommt.

Abb. 6:

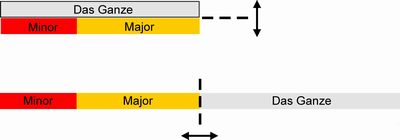
• Oben:

  Das Ganze steht als separate Größe über dem Grundverhältnis.

• Unten:

  Nebeneinander gestellt sind die drei Größen Minor, Major und das Ganze. Die nun vertikale Symmetrieachse zeigt den eindrücklichen Zusammenhang des asymmetrischen Grundverhältnisses des goldenen Schnittes mit der Symmetrie. Diese lineare Abfolge entspricht dem Nebeneinander der Fibonacci-Zahlen, wie wir noch sehen werden.

Der goldene Schnitt verbindet so auf eindrückliche Weise das Prinzip der Symmetrie mit dem der Asymmetrie. Diesen »verbindenden« Eigenschaft der auch als »göttliche Proportion« bezeichneten Gesetzmäßigkeit werden wir in den folgenden Beispielen immer wieder erfahren. So wird offensichtlich, dass der goldene Schnitt wegen seines »die Gegensätze verbindenden Charakters« als schön und harmonisch empfunden wird.

Rechnet man nun mathematisch aus, in welchem Verhältnis Minor zu Major und dieser zum Ganzen stehen, so ergibt sich folgende Zahl, die als Konstante Phi bezeichnet wird:

Φ = 1,618033988749894848204586834365638117720309179805762862135...

Sie besagt, dass beispielsweise der Major 1,61...fach größer ist als der Minor, und wiederum dass das Ganze 1,61..mal größer ist als der Major. Diese nach dem Komma endlose Zahl gehört zur Gruppe der irrationalen Zahlen. Gerade ein solches irrationales Zahlenverhältnis wird als besonders harmonisch und schön empfunden. Ein scheinbar weiterer Widerspruch, denn ist nicht in aller Regel gerade das Irrationale das, was den Menschen beunruhigt und was er mit Hilfe seiner Rationalität zu beseitigen versucht?

Der Parthenon zu Athen

Seit Menschengedenken finden wir die goldene Proportion überall dort, wo Menschen Schönheit zum Ausdruck bringen wollten und wo sie sich dem göttlichen Ideal anzunähern versuchten. Dies sind im Allgemeinen die Kunst und im Besonderen ihre heiligen Stätten, die Tempel.

Der Parthenon zu Athen zählt zu einem der bekanntesten klassischen Bauten. Er gilt gleichzeitig als das schönste und vollendetste Werk der antiken griechischen Architektur. Dieser berühmte Tempel, der als Krönung für die gesamte Akropolis steht, wurde rund 450 v. Chr. unter Perikles errichtet. Er gilt bis heute als ein Paradebeispiel klassischer symmetrischer Baukunst. Die exakt symmetrische Anordnung der einzelnen Elemente findet sich bis in kleine Details, aus allen Perspektiven, wieder. Neben der Symmetrie sind aber auch die Proportionen des goldenen Schnittes in vielfacher Art und Weise und erstaunlicher Genauigkeit verbaut. Die stilisierten Grafiken (Abb. 7 und 8) sollen dies nur beispielhaft erläutern. Abbildung 7 zeigt in einer vertikalen Unterteilung das Verhältnis zwischen Unter- und Überbau des Tempels. Der Überbau reicht vom Giebel bis zu den tragenden Säulen, zum Unterbau gehört der tragende Teil, also die Säulen und Stufen. Beide Teile des Bauwerks stehen in beeindruckend exakter Art und Weise im Verhältnis des goldenen Schnittes.

Abb. 7: Das Verhältnis von Über- zu Unterbau des Parthenon spiegelt exakt die Proportionen des goldenen Schnittes wieder.

In Abbildung 8 wird die Höhe (Grundlinie der Treppe bis zur Spitze des Giebels) zur Breite (Breite des Aufbaus) des Bauwerks ins Verhältnis gesetzt. Höhe und Breite verhalten sich ebenso wie Minor zu Major. Eine solche flächenhafte Ausdrucksweise des goldenen Schnittes wird auch als goldenes Rechteck bezeichnet.

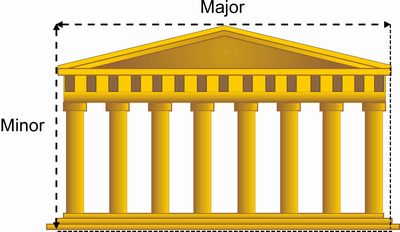Abb. 8: Höhe und Breite des Parthenon verhalten sich wie Minor und Major.

Neben der Umsetzung des goldenen Schnittes finden sich jedoch auch noch zahlreiche andere asymmetrische Details im Parthenon. An vielen Stilelementen des Bauwerks sind bewusst Symmetriebrüche eingebaut. So stehen beispielsweise die Säulen nicht gerade, sondern sind leicht nach innen gebogen. Auch stehen sie bei genauer Vermessung keineswegs an den einer Symmetrie entsprechenden Punkten. Von diesen weichen sie vielmehr deutlich ab, was dem profanen Auge allerdings unsichtbar bleibt.

All diese Details zeigen schließlich, dass der Parthenon eine Symbiose von Symmetrie und Asymmetrie ist. Ähnlich wie im goldenen Schnitt an sich Symmetrie und Asymmetrie in Verbindung stehen, so kommen auch in jeder materiellen Umsetzung des Prinzips diese Qualitäten des Ausgewogenen wieder zum Vorschein.

Der Parthenon ist nur ein Beispiel unter vielen für die Anwendung des goldenen Schnittes in berühmten und großen sakralen Bauten. Die Umsetzung menschlichen Schönheitsempfindens in Form des goldenen Schnittes findet sich in zahlreichen anderen bekannten Bauwerken, wie der alten Petersbasilika in Rom oder dem Kölner Dom wieder (Moessel 1926). Selbst in den Pyramiden von Gizeh zeigen sich die Proportionen der Zahl Phi in erstaunlicher Genauigkeit (Hagenmaier 1988). So ist beispielsweise der Neigungswinkel der Cheops-Pyramide a = 51°50’ bis a = 51°52’. Der Kosinus dieses Winkels beträgt 0,618. Auf die gleiche Größe stößt man beim Verhältnis der Länge der Pyramidenseite zur Hälfte der Pyramidenbasis (356 : 220 Ellen). Auch im berühmtesten der großen Steinmonumente, Stonehenge, das vor ca. 3500 Jahren bei Salisbury in England erbaut wurde, finden sich die goldenen Maße wieder (Doczi 1996). In der Kunst zeigen sich die Proportionen des goldenen Schnittes im Grundaufbau zahlreicher bekannter Gemälde (Doczi 1996), wie »Das Abendmahl« von Leonardo da Vinci, Albrecht Dürers »Selbstbildnis« oder Raffaels »Die Sixtinische Madonna«.

Die goldenen Proportionen sind jedoch nicht nur Produkt eines bewusst menschlichen Schaffens, wie die zahlreichen oben erwähnten Beispiele vermuten lassen. Sie scheinen ursprünglicherer Natur zu sein.

Die Steinkeile

Die sogenannten Stein- oder Faustkeile sind Artefakte früher Menschen. Sie stammen aus einer Zeit vor etwa 0,5 bis 1,3 Millionen Jahre. Es handelt sich um von Menschen geschlagene Steine, deren Abschläge als Werkzeuge gebraucht wurden. Der Steinkeil an sich ist das Mutterstück der zahlreichen abgeschlagenen Werkzeug-Geräte. Vermutlich wurde er als eine Art Kultobjekt besonders behandelt. Die Steinkeile aus Kilombe, einer Fundstelle in Kenia, wurden von Archäologen vermessen. Sie kommen dort in verschiedenen Größen, aber immer ähnlichen Grundformen vor.

Das Ergebnis der Vermessungen demonstriert Abbildung 9 (Gowlett 1985). In Bezug zueinander wurden Länge und Breite verschieden großer Keile gesetzt. Trotz unterschiedlicher Größe zeigt sich eine Besonderheit: Anhand der mittelnden Geraden wird deutlich, dass die Proportionen von Länge und Breite zwischen den verschieden großen Steinkeilen beeindruckenderweise immer annähernd gleich sind. Die Schlussfolgerung ist faszinierend: Bereits vor 1 Million Jahren bevorzugte der Homo erectus eine bestimmte Proportion, die er in den Steinkeilen unbewusst umsetzte. Eine Berechnung des Verhältnisses zeigt, dass es sich hierbei sehr genau um die Proportionen des goldenen Schnittes handelt. In einer Zeit, als es weder ein Zahlensystem, geschweige denn ein Maßsystem gab, wurden die Steine sicherlich nicht bewusst in diesen Proportionen geschlagen. Dennoch findet sich ein annähernd einheitliches Größenverhältnis der Steinkeile. Dies lässt zweifelsfrei die Schlussfolgerung zu, dass die Verhältnismäßigkeiten des goldenen Schnittes schon in früher Menschheitsentwicklung empfunden wurden. Der goldene Schnitt ist demnach nicht nur eine bewusste Erfindung des Menschen, wie er beispielsweise im Parthenon zum Ausdruck kam, sondern ursprünglicher, allgemeingültiger Art und Natur. Der Homo erectus brachte unbewusst eine tiefgreifende Gesetzmäßigkeit zum Ausdruck.

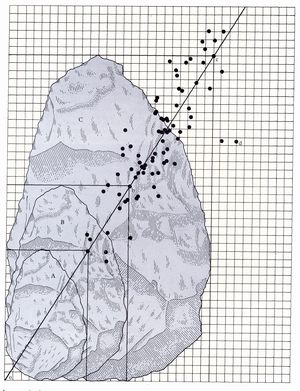Abb. 8: Die Proportionen verschieden großer Steinkeile (A, B, C) sind immer annähernd gleich. (Aus Gowlett 1985)

Sowohl der Parthenon als auch die Steinkeile haben ihren Ursprung deshalb in einem subjektiven Schönheitsempfinden des Menschen. Dies legt die Vermutung nahe, dass der goldene Schnitt nur ein Produkt des Menschen, ein Ausdruck seines subjektiven Schönheitsempfindens ist. In den letzten 2 Jahrhunderten hat sich jedoch mit der Entwicklung und Verbesserung naturwissenschaftlicher Untersuchungsmethoden herausgestellt, dass die Zahl Phi und der goldene Schnitt objektiv in der Natur vorkommen.

Die Proportionen des menschlichen Körpers

Vor rund 150 Jahren beschäftigte sich der Mediziner Adolf Zeising mit den Maßen des menschlichen Körpers. Mit dem Ziel, eine übergreifende Gesetzmäßigkeit in Bezug auf den Bau des menschlichen Körpers zu finden, vermaß er zahlreiche Menschen und deren Körperteile. Er verglich sie untereinander und mit bekannten klassischen Statuen der Antike, von denen man bis heute sagt, dass sie ein perfektes Bild des menschlichen Körpers zur Darstellung bringen. Die Ergebnisse veröffentlichte er in seinem Lebenswerk »Neue Lehre von den Proportionen des menschlichen Körpers« (1854). Sie sollen im Folgenden anhand weniger Beispiele erläutert werden. Zur Darstellung der Größenverhältnisse und Gliederung der einzelnen Körperabschnitte des Menschen wird die griechische Statue des Speerträgers des Doryphoros von Polyklet herangezogen.

Abbildung 10 zeigt eine Unterteilung der Gesamtkörpergröße der Statue (vom Scheitel bis zur Fußsohle) nach den Verhältnissen der Zahl Phi. Wird der untere Teil als Major und der obere als Minor angenommen, so verläuft die Trennungslinie beider Abschnitte in der Höhe des Bauchnabels, genauer, durch die unmittelbar in Höhe des Nabels verlaufende Bauchfalte; die sogenannte Nabelfalte, secunda inscriptio tendinea musculi recti abdominis. Eindrucksvoll ist, dass diese Aufteilung in Ober- und Unterkörper auch am bekleideten Menschen seit je durch den Gürtel hervorgehoben wird. Auch hier besteht wieder eine Verbindung zwischen den Proportionen des goldenen Schnittes und dem subjektiven Schönheitsempfinden des Menschen, der offensichtlich unabhängig von wechselnden Schönheitsidealen diese Trennungslinie durch seine Kleidung seit Jahrtausenden betont. Zeising weist auf die Besonderheit hin, dass gerade der nährende Nabel der Ausgangspunkt jeder menschlichen Leibesentwicklung ist.

Ausgehend von dieser Grundteilung des menschlichen Körpers demonstriert Zeising weitere Aufgliederungen nach den Maßen des goldenen Schnittes. Abbildung 11 zeigt die Einteilung von Ober- und Unterkörper nach dem gleichen Prinzip. Bei der Teilung des Oberkörpers im goldenen Schnitt stellt sich die Trennungslinie in Höhe des Kehlkopfes dar. Anatomisch exakt beschrieben läuft die Trennlinie genau durch den Winkel, der durch den Musculus sternocleidomastoideus und den Musculus cucularis gebildet wird. Der Oberkörper wird demnach in zwei Partien, die Kopfpartie und die Rumpfpartie, geteilt. Im Unterkörper fällt die Trennlinie nicht genau durch das Kniegelenk, sondern exakt auf die Stelle, an welcher sich die Fibula sichtbar von der Tibia scheidet. Es ist die Stelle, an der das Bein zwischen Hüfte und Wade die geringste Breite besitzt; ähnlich der Einbuchtung der Hüfte oder des Halses, welche die Trennungslinie für den Gesamt- beziehungsweise den Oberkörper sind.

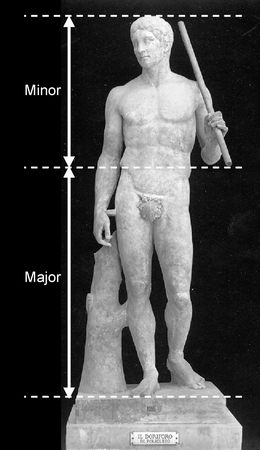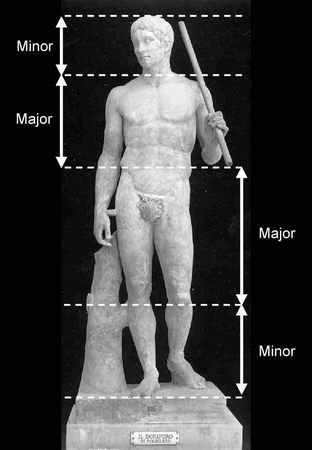Abb. 10: Unterteilung des menschlichen Körpers nach den Proportionen des Goldenen Schnitts, exemplarisch anhand der Statue des Doryphoros	Abb. 11: Einteilung des Ober- sowie des Unterkörpers nach den Proportionen des Goldenen Schnittes

Zeising hat die Proportionen des goldenen Schnittes bis ins kleinste Detail am menschlichen Körper aufgezeigt. Die anatomische Genauigkeit dieses Verhältnisses bei der Gliederung des Menschen ist dabei äußerst beeindruckend. Heutzutage ist das Wissen darum insbesondere bei der Wiederherstellung bestimmter Körperteile sehr nützlich geworden. Praktische Relevanz finden die Proportionen des goldenen Schnittes vor allem in der modernen Schönheitschirurgie (Marquardt 2002) und in der Zahnmedizin bei der Herstellung harmonisch wirkender Zahnformen (Levin 1978, Javaheri & Shahnavaz 2002). So ist beispielweise bekannt, dass die Breiten der ersten beiden oberen Schneidezähne im Verhältnis 1 : 1,618 stehen (Abb. 12)

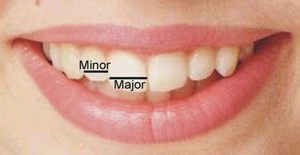Abb. 12: Die Breiten des ersten und zweiten oberen Schneidezahnes verhalten sich zueinander wie Major zu Minor.

An dieser Stelle soll daran erinnert werden, dass auch beim Menschen die Proportionen des goldenen Schnittes immer mit dem Prinzip der Symmetrie auftreten: Während beim Aufbau des menschlichen Körpers die vertikale Gliederung vornehmlich nach den Proportionen des goldenen Schnittes erscheint, so zeigt sich in der horizontalen vor allem das Prinzip der Seitengleichheit, der Symmetrie. Das Zusammenspiel von Symmetrie in der horizontalen und Asymmetrie in der vertikalen Ebene lässt sich gut am Beispiel der Zähne nachvollziehen. Wie der goldene Schnitt an sich, ist auch der Mensch Ausdruck von Symmetrie und Asymmetrie.

Die Fibonacci-Reihe

Das Auftreten dieser Proportionen am menschlichen Körper zeigt, dass der goldene Schnitt nicht nur ein Produkt der Kunst ist, sondern dass im Laufe des 19. und 20. Jahrhunderts bewiesen werden konnte, dass der goldene Schnitt in zahlreichen Wachstumsmustern von Pflanzen, Tieren und Mensch naturgemäß vorkommt. In der Natur sind die Proportionen des goldenen Schnittes also in vielfacher Art und Weise vorhanden.

Anfang des 19. Jahrhunderts untersuchten die befreundeten Botaniker Alexander Braun und Carl Schimper die Wachstumsgeometrien in der Pflanzenwelt. Die wichtigste Erkenntnis war, dass sich bei genauer Betrachtung der Abfolge der Blätter am Stängel einer Pflanze immer wieder ganz bestimmte Blattanordnungen fanden, die das höhere Pflanzenreich durchziehen. Dabei werden eine gegenständige, symmetrische und eine asymmetrisch, spiralige Blattstellung voneinander unterschieden. Bei der symmetrischen Anordnung stehen sich jeweils zwei Blätter gegenüber. Bei der asymmetrischen Blattstellung sind die einzelnen Blätter nicht etwa willkürlich, sondern im Rahmen einer bestimmten Spiraltendenz angeordnet. Innerhalb der asymmetrischen, spiraligen Blattgeometrie zeigten sich nun ganz bestimmte Zahlenverhältnisse. Dies lässt sich folgendermaßen erläutern:

Bei der asymmetrischen Blattstellung sind die Blätter am Stängel einer Pflanze nicht in zufälliger, unregelmäßiger Reihe angeordnet, sondern folgen regelmäßig aufeinander. Aufgrund der Regelmäßigkeit im Spiralzyklus werden diese Blattstellungen auch als zentralsymmetrisch bezeichnet. Das heißt jedes Blatt bildet zum nächst höheren einen bestimmten Winkel (Divergenz). Folgt man der Anordnung der Blätter, so wird man spiralig um den Stiel herumgeführt. Erst ein ganz bestimmtes Blatt zeigt dann wieder in die gleiche Richtung wie das erste Blatt. Bis zu dieser Ausgangsstellung wird eine bestimmte Anzahl von Windungen zurückgelegt. Dies wird als Blattzyklus bezeichnet und in Bruchzahlen angegeben. Winden sich beispielsweise fünf Blätter in zwei Windungen um den Stiel bis die Ausgangsstellung, das heißt der »Ursprung«, wieder erreicht ist, dann spricht man von einem Blattzyklus von 2/5. Hinter der offensichtlich asymmetrischen Blattanordnung verbirgt sich demnach doch wieder eine Regelmäßigkeit, eine Symmetrie.

Im Pflanzenreich kommen verschiedene Arten von Blattzyklen vor. Äußerst beeindruckend ist allerdings, dass bestimmte Blattzyklen immer wieder vorkommen, andere Kombinationen dagegen gar nicht. So gibt es beispielsweise keine Pflanze, bei der die Anzahl der auf einen Zyklus kommenden Blätter 12, 15 oder 20 beträgt! Trägt man das gesamte Spektrum der verschiedenartigen, tatsächlich in der Natur vorkommenden Blattzyklen zusammen, so entsteht folgende Reihe:

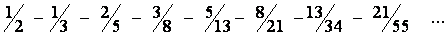
Sie weist eine eigenartige Besonderheit auf: Es handelt sich bei der Zahlenreihe sowohl im Nenner als auch im Zähler jeweils um die gleiche Folge von Zahlen, lediglich um zwei Stellen verschoben. Diese Zahlenfolge wird auch als die Fibonacci-Reihe bezeichnet:

Die Fibonacci-Folge wurde das erste Mal von dem italienischen Mathematiker Leonardo von Pisa (Abb. 13), genannt Fibonacci, im Jahre 1202 in seinem Buch »Liber Abaci« veröffentlicht. Mit diesem Werk führte er das indisch-arabische Dezimalzahlensystem in Europa ein.

Abb. 13: Leonardo von Pisa, genannt Fibonacci

Weitere Untersuchungen zeigten, dass sich die Fibonacci-Reihe auch noch in zahlreichen anderen Wachstumsvorgängen der Pflanzen manifestiert. So finden sich diese Zahlen beispielsweise in der Struktur vieler Blüten wieder. Die Ähnlichkeit zum Blattzyklus verwundert nicht. Bereits Goethe vermutete in seiner Metamorphose der Pflanze ein einheitliches Wachstumsprinzip von Blatt, Stängel und Blüte einer Pflanze. Eindrücklich sind diese Zahlenverhältnisse am Beispiel der Sonnenblume zu demonstrieren. Ihrer besonderen Größe wegen ist die beeindruckende Anordnung besonders gut zu erkennen (Abb. 14): Das gesamte Blütenkörbchen besteht aus zahlreichen kleinen echten Blüten. Diese sind jedoch nicht chaotisch angeordnet, sondern in deutlich erkennbaren Spiralzügen. Hier wird ersichtlich, dass innerhalb einer Blüte rechtsdrehende und linksdrehende Spiralzüge existieren. Die Anzahlen der Spiralzüge sind erstaunlicherweise wiederum nicht beliebig. Bestimmte Zahlen treten immer wieder auf. Dabei handelt es sich stets um Glieder aus der Fibonacci-Reihe! Bei großen Sonnenblumen findet sich beispielsweise ein Verhältnis von 89 zu 144 oder sogar 144 zu 233 Spiralzügen.

Abb. 14: Der Blütenkorb der Sonnenblume besteht aus zahlreichen kleinen Blüten, die in mehreren rechts- und linksdrehenden Spiralen angeordnet sind. Die Anzahlen der Spiralen sind immer Glieder der Fibonacci-Reihe (hier 21 und 34).

Die Fibonacci-Zahlen finden sich auch in der Schuppenordnung von Tannenzapfen, der Anordnung der Stacheln von Kakteen, beim Aufbau der Ananasfrucht usw. Es scheint, als sei die Fibonacci-Reihe eine Art Wachstumsmuster in der Natur. Die Fibonacci-Zahlen weisen zudem einige sehr eindrückliche mathematische Besonderheiten auf:

• Jede Zahl der Folge ist die Summe der beiden vorausgehenden Zahlen (Abb. 15). Die Reihe folgt demnach einem Additionsgesetz. Jede Zahl hat eine Beziehung zur vorherigen Zahl und zur folgenden Zahl. Ähnlich wie Major eine Beziehung zu Minor und dem Ganzen hat. Wachstum in der Natur scheint einem zeitlichen Bezugsgesetz, einem Additionsgesetz, zu folgen!

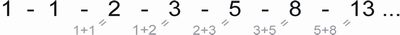• Abb. 15: Jede Zahl der Fibonacci-Reihe ist die Summe der beiden vorausgehenden Zahlen.

• Noch erstaunlicher ist, dass diese Zahlenfolge in einem unmittelbaren Zusammenhang zum goldenen Schnitt steht. Die Verbindung ist einfach und eindrücklich: Das Verhältnis zweier aufeinander folgender Fibonacci-Zahlen nähert sich immer mehr dem Verhältnis des goldenen Schnittes, der Zahl Phi, an. Je mehr Spiralzüge beispielsweise der Blütenkorb einer Sonnenblume aufweist, um so mehr nähert sich das Verhältnis der einbezogenen Fibonacci-Zahlen dem goldenen Schnitt an. Mathematisch ausgedrückt, entspricht der Grenzwert (Limes) zweier aufeinander folgender Zahlen der Fibonacci-Folge exakt dem Verhältnis des goldenen Schnittes, der Zahl Phi!

• 21 : 13 = 1,615434 : 21 = 1,619055 : 34 = 1,6176 ... » 1,618033 (Φ)

• Die nebeneinanderstehenden Fibonacci-Zahlen nähern sich in ihrem Verhältnis zueinander nicht beliebig dem Wert des goldenen Schnitts (Φ) an. Sie tun es abwechselnd von oben und von unten (Abb. 16). Dadurch werden zwei voneinander unterschiedene Reihen beschrieben. Die eine Reihe nähert sich von oben dem Wert Phi an, die andere von unten. Sie bilden eine polare Gegenläufigkeit, die auf eine gemeinsame Einheit zulaufen, deren Repräsentant die Zahl Phi ist. Die Fibonacci-Reihe folgt damit inhaltlich wiederum dem Prinzip der Symmetrie.

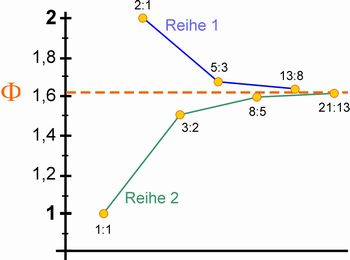• Abb. 16: Das Verhältnis zweier aufeinander folgender Fibonacci-Zahlen nähert sich symmetrisch in zwei Reihen, abwechselnd von oben und unten, immer mehr der Zahl Phi an.

Alles in allem gilt heute die Fibonacci-Reihe als ein anerkanntes Wachstums- und Entwicklungsmuster in der Pflanzenwelt. Auch der Zusammenhang zu den Proportionen des goldenen Schnittes ist unbestritten. Es fällt nun schwer, aus diesen Zusammenhängen nicht die Schlussfolgerung zu ziehen, dass es sich hier um eine der Urformen natürlicher Prozesse handelt. Der in den USA lebende ungarische Architekt und Botaniker Györgi Doczi, der sehr ausführlich und eindrucksvoll den goldenen Schnitt als universelles Ganzheitsmuster in der Natur belegt hat, schreibt angesichts dieser Erkenntnisse (G. Doczi, in: Gowlett 1985): »Auch wir, die wir uns nicht mehr vor rachsüchtigen Göttern fürchten, empfinden Ehrfurcht und Staunen angesichts dieser unerwarteten Präzision eines Wachstumsmusters der Natur.«

Das Beispiel der Fibonacci-Reihe zeigt, dass der goldene Schnitt nicht nur das Produkt menschlichen Schönheitsempfindens ist, sondern als objektives Entwicklungsmuster in der Natur vorkommt. An dieser Stelle wird Goethe schon verständlicher mit seiner Behauptung, dass Schönheit eine Manifestation von Naturgesetzen ist. Biologen vermuten, dass die Fibonacci-Reihe und der goldene Schnitt vor allem deswegen optimale Entwicklungs- und Konstruktionsprinzipien sind, da sie Ausdruck einer maximalen Vereinfachung numerischer Beziehungen sind (Radiuk 2001). Der goldene Schnitt als einfachste Urform jeglicher Gestaltung? Eine mathematische Analyse verdeutlicht dies.

Die Mathematik

Erwähnenswert sind vor allem zwei mathematische Besonderheiten im Zusammenhang mit der Zahl Phi:

a) Die Besonderheit der Zahl

Die Maßzahl des goldenen Schnitts gehört zu den irrationalen Zahlen, das heißt sie ist nicht durch Brüche ganzer Zahlen darstellbar, wie zum Beispiel 1/3. Nun scheint es, als wären alle irrationalen Zahlen gleich irrational, aber einige irrationalen Zahlen sind irrationaler als andere. Das lässt sich folgendermaßen verstehen: Wenn man das Maß für die Irrationalität darin sieht, inwieweit man sie mit Hilfe von rationalen Zahlen in die Nähe dieser irrationalen Zahl bringen kann, dann lassen sich verschiedene Stufen der Irrationalität beschreiben. In der so entstehenden Kette der irrationalen Zahlen bildet die goldene Zahl Phi das Schlusslicht. Phi ist die irrationalste aller irrationalen Zahlen! Das wirkt erst einmal erstaunlich, denn es besagt nichts anderes, als dass wir gerade das Irrationalste als besonders harmonisch empfinden. Das von uns als wohlproportioniert Empfundene ist nicht nur das Gegenteil des Rationalen, es hat sogar eine maximale Entfernung zu ihm. Wir erfahren hier gerade das Gegenteil dessen, was uns die formale Logik glauben macht. Hier berühren sich die Extreme, Rationalität und Irrationalität, Schönheit und Chaos. Das Irrationale, nicht vollständig Erfassbare findet sich nicht etwa im Ungeordneten, Unangenehmen, wie man meinen würde, sondern ist darüber hinaus auch noch Ausdruck des Schönen und Wohlproportionierten. Wieder treffen bei der Betrachtung des goldenen Schnittes scheinbar widersprüchliche Qualitäten aufeinander. Einmal mehr wird deutlich, dass dieses Zahlenverhältnis bei der Vereinbarung von Gegensätzen eine besondere Rolle zu spielen scheint. Die rein mathematische Betrachtung der Zahl Phi macht ihre Sonderstellung innerhalb der Zahlen offensichtlich.

b) Die »schöne« Formel

So lässt sich über die Verhältnismäßigkeiten der drei Größen Minor, Major und das Ganze eine einfache Formel für die Berechnung der Zahl Phi ableiten. Abbildung 17 zeigt die klassische und gleichzeitig bekannteste Formel zur Ermittlung der Proportionen des goldenen Schnittes.

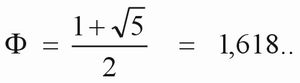Abb. 17: Die »klassische« Formel zur Berechnung der Zahl Phi

Neben der erwähnten gibt es noch eine weitere Formel zur Berechnung der Zahl Phi, die bis heute, selbst in mathematischen Kreisen, noch meist unbekannt ist. Jeder mathematische Bruch ist durch sogenannte »Kettenbrüche« darstellbar (Peitgen & al. 1992). Das gilt wohlgemerkt für jede Art von Bruch! Bei Kettenbrüchen handelt es sich um Simplifizierungen des ursprünglichen Verhältnisses durch eine Aufschlüsselung in mehrere einfache Brüche. Abbildung 18 zeigt ein solches Beispiel. Zähler jedes einzelnen Bruches ist die Zahl Eins. Auch dies gilt für alle denkbaren Brüche und Verhältnisse! In Bezug zur Zahl Eins ist demnach jedes rationale Verhältnis darstellbar.

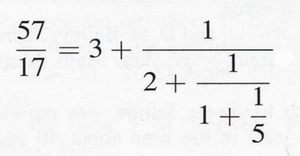Abb. 18: Beispiel für eine Kettenbruchdarstellung eines bestimmten Verhältnisses

Neben allen normalen Zahlen und Bruchzahlen ist auch jede irrationale Zahl durch einen Kettenbruch darstellbar. Der einzige Unterschied besteht darin, dass Kettenbrüche irrationaler Zahlen unendlich lange Wiederholungen eines gleichen Grundelements sind. Abbildung 19 verdeutlicht dies anhand der irrationalen Zahl Ö2. Der Kettenbruch ist demnach ein mathematisches Verfahren, mit welchem jede Zahl und jedes Zahlenverhältnis ausgedrückt werden kann. Auch die irrationale Zahl Phi ist in Form eines Kettenbruches darstellbar. Dabei ergibt sich folgende, höchst einfache Formel für die Berechnung der Zahl Phi (Abb. 20).

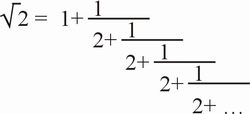Abb. 19: Kettenbruchdarstellung einer irrationalen Zahl, hier am Beispiel der Ö2

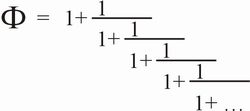Abb. 20: Kettenbruchdarstellung der Zahl Phi

Die Zahl des goldenen Schnittes zeigt damit innerhalb der Kettenbruchdarstellungen eine einzigartige Stellung: Der Kettenbruch zur Berechnung der Zahl Phi besteht als einziger unter allen denkbaren aus nur einer Zahl! Damit aber nicht genug. Der goldene Schnitt errechnet sich darüber hinaus aus der Zahl Eins. Die Zahl Phi ist demnach »Ausdruck der Zahl Eins«. Es kann also auf die Besonderheit hingewiesen werden, dass die irrationalste Zahl sich durch den einfachsten Kettenbruch errechnet! Das Irrationalste lässt sich nicht etwa nur durch einen komplizierten mathematischen Zusammenhang beschreiben, sondern ist vor allem Ausdruck einer der einfachsten Verhältnisse – Ausdruck der einfachsten Zahl! Die oben erwähnte Vermutung, dass der goldene Schnitt aufgrund seiner maximalen Simplifizierung das Urverhältnis jeglicher Zusammenhänge darstellt, wird evident. Die goldenen Proportionen und ihre unmittelbare Erscheinung in der Fibonacci-Reihe sind Ausdruck einer maximal vereinfachten Information, die ausschließlich durch die Zahl Eins und das Additions- wie Divisionsgesetz beschrieben wird. Die Natur bevorzugt dieses Verhältnis in zahllosen Erscheinungen. Es muss sich demnach um ein Lebens- und Entwicklungsprinzip schlechthin handeln.

Eine andere Ausdrucksweise für die gleiche Formel zeigt Abbildung 21.

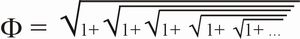Abb. 21: Einfache Formel zur mathematischen Darstellung der Zahl Phi

Auch diese zweite Herleitung spart nicht an Kuriositäten. Sie zeigt in etwa die gleichen mathematischen Eigenarten wie die Kettenbruchdarstellung der Zahl Phi. Die Formel unterliegt im Aufbau dem gleichen Prinzip, wie es durch die geometrische Ausdrucksweise des goldenen Schnittes (Abb. 4 und 6) zum Vorschein kommt. So wie Minor eine Beziehung zum Major hat, so hat auch in der Formel jedes Element eine Beziehung zum über- und zum untergeordneten Element. Jedes nächste Glied steht unter dem Wurzelzeichen des vorhergehenden. Damit besteht immer ein Zusammenhang zum nächsthöheren, ähnlich der stetigen Beziehung vom Minor zum Major. Gerade das besondere Verhältnis des Ganzen und seiner Teile zueinander ist ja Entstehungsweise des goldenen Schnittes. Als weitere Besonderheit darf gelten, dass es sich bei der Rechenoperation immer auch um Additionen handelt. Der goldene Schnitt ist Ausdruck eines Additionsverhältnisses, wie wir ihm bereits als Grundprinzip innerhalb der Fibonacci-Reihe begegnet sind. Man kann schlicht sagen: Die Formel ist schön.

Die mathematischen Ausführungen zeigen auf imposante Art, dass der goldene Schnitt und die Zahl Phi eine »unbezweifelbar zentrale Rolle innerhalb der Mathematik« einnehmen (Beutelspacher & Petri 1995). Das Rätsel ihrer elitären Stellung innerhalb der Mathematik war bisher allerdings ungeklärt. Es ist anzunehmen, dass sich eine befriedigende Erklärung der Sonderstellung der Zahl Phi nicht allein aus einer mathematischen Analyse finden lässt. Denn die Kenntnis der mathematischen Regeln, mit denen der goldene Schnitt errechnet oder geometrisch konstruiert wird, bedeutet ja noch nicht, seinen inhaltlichen Charakter erfahren zu haben. Die mathematischen Zusammenhänge können jedoch helfen, den Zugang zum universalen Charakter der Proportio divina und seiner eindrücklichen Verbindung zur Schönheit zu finden. Carl Friedrich von Weizsäcker vermutete, »vielleicht ist die allgegenwärtig verborgene Mathematik der Natur der Seinsgrund aller Schönheit.« (von Weizsäcker 1995)